Name____________________________________________________________________ Period____________

1. A potter’s wheel of radius 0.50 m and mass of 100.0 kg is freely rotating at 50.0 rev/min. The potter can stop the wheel in 6.0 s by pressing a wet rag against the rim and exerting a radially inward force of 70.0 N. What is the angular acceleration of the wheel?

There are 2 pi radians in a full revolution. So in 50 rotations there are

It takes it 1 minute to do these 50 rotations, or 100 pi radians. So the angular speed

Of the wheel is 100 pi rad/min.

But in Physics, we like rad/s

Dividing by 60 gives us radians per second.

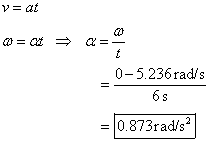
2. Calculate the following:

a. The angular momentum of the Earth due to its spinning motion on its axis

Earth’s angular speed is 2 pi radians per day, or 2 pi radians per 86400 seconds.

Earth can be approximated as a solid sphere. According to Hewitt’s chart, a solid sphere has a moment of inertia of a solid sphere is

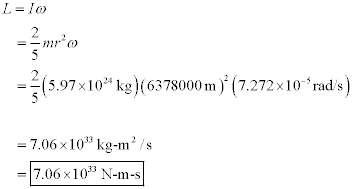
b. The angular momentum of the Earth from its orbital motion around the Sun.

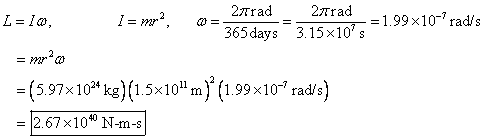
3. A skater spins with an angular speed of 12.0 rad/s with her arms outstretched. She lowers her arms, decreasing her moment of inertia from to . Calculate her initial and final rotational kinetic energy. How do you account for the change in kinetic energy?

A) Her initial rotational energy is

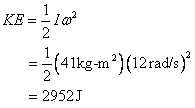
B) Her angular momentum is

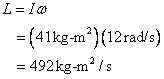
C) Angular momentum is conserved. That means it does not change when she pulls her arms in. Therefore, her angular momentum after she has pulled her arms in is still 492 kg-m²/s. However, her moment of inertia has changed. So for L to remain constant, her angular velocity, ω, must also change.

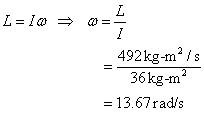
D) So her final rotational kinetic energy is

It took energy for her to pull her arms in. This energy came from chemical potential energy in her muscles. That energy came from the food she ate. That energy came from the sun, which provided light for the vegetables she ate to photosynthesize. So the extra energy came from the sun.